Parabolas Lesson 5 Episode 5 (Teachers)

Sasha and Keoni notice a pattern in the denominators of their three equations (y = x²/4, y =  x²/8, and y =  x²/12); yet they  struggle to determine how the pattern is being generated [0:41- 0:50].

➤ Sasha and Keoni first plot the focus and directrix for each parabola. They then make sense of a pattern that relates the distance between the focus to the vertex to each equation.

For use in a classroom, pause the video and ask these questions:

1. [Pause video at 0:46]. What have Sasha and Keoni already figured out about the equations of the parabolas?

2. [Pause video at 6:21]. What do you think about Sasha and Keoni’s conjecture? How did they arrive at it?

Provide an opportunity for students to revoice other student’s ideas in the classroom.

1. As students answer Focus Question 2, ask students to revoice the ideas of their classmates.

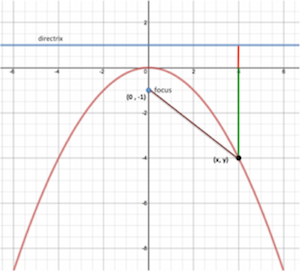
The graph below represents a parabola with a focus at (0, –1) and a directrix at y = 1. A general point on the parabola is labeled as (x, y). The distance between that point and the focus is shown in brown. The distance from the general point to the directrix is represented by the red and green segments together.

1. Can the value of y for any point (x, y) on this parabola be positive? Why or why not?

2. The distance from the point (x, y) to the x-axis (shown by the green segment) is -y. Explain why. Hint: Consider the distance from different points on this parabola, like (2,–1) or (4,–4), to the x-axis.

 3. Use the definition of a parabola and the Pythagorean theorem, find the general equation for the parabola. Show your work.