Home
Episode 2 Supports
Episode Description
Exploring: Keoni and Sasha use the Pythagorean Theorem and the definition of a parabola to derive an equation of parabola with a p-value of 5 and a vertex at (9, 13).
Students’ Conceptual Challenges
At [0:48], Keoni is unsure whether to draw a segment from the general point to the vertex or to the focus.
- Sasha and Keoni resolve the issue by reminding themselves of the definition of a parabola. They recall how they can use the definition to represent the lengths of the sides of a right triangle.
- Sasha and Keoni resolve the issue by reminding themselves of the definition of a parabola. They recall how they can use the definition to represent the lengths of the sides of a right triangle.
Focus Questions
For use in a classroom, pause the video and ask these questions:
1. [Pause the video at 1:54]. What is the distance y? How would you represent it geometrically on the coordinate grid?
2. [Pause the video at 3:46]. What are the coordinates of the third vertex of the triangle?
Supporting Dialogue
Invite students to engage in productive disagreement:
- As Sasha and Keoni are completing their algebraic manipulations, Sasha cancels the 20 [7:34]. But then it shows up in the final version of the equation. What happened? Did she make a mistake?
Math Extensions
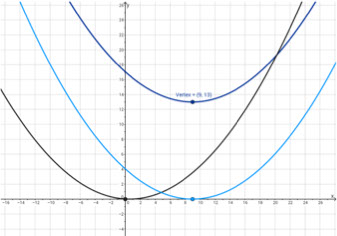
In the graph below, the base parabola with p =5, shown in black, is represented by the equation y = x2/20. If the base parabola is translated to the right 9 units, it will be the parabola shown in light blue, which is represented by the equation y = (x–9)2/20. If this parabola is translated up 13 units, it will be the parabola shown in dark blue, which is represented by the equation y = (x–9)2/20 + 13.
- Use the equations to prove that each vertex is on a particular parabola; what do you notice?
- Use the equations to find a “special point” (a point aligned horizontally with the focus) for each parabola; what do you notice?
Mathematics in this Lesson
Lesson Description
Targeted Understanding
CC Math Standards
CC Math Practices
Lesson Description
Sasha and Keoni develop the vertex form of the equation of a parabola as y = (x–h)2/(4p) + k where the (h,k) is the vertex and p the distance from the vertex to the focus.
Targeted Understandings
This lesson can help students:
- Derive the vertex form of the equation of a parabola by using the method developed in previous lessons (which involves the definition of a parabola and the Pythagorean theorem), but generalizing from working with particular vertices to an unknown vertex (h,k) and generalizing from a specific distance from the vertex to the focus to an unknown p-value.
- Interpret algebraic expressions involving parameters (x – h, y – k , and y – k – p) as distances on a coordinate grid.
- Conceive of algebraic expressions, such as x – h, as both a single entity and as a process of subtracting the value of one variable from the value of another.
Common Core Math Standards
• CCSS.M.HSG.GPE.A.2: Derive the equation of a parabola given a focus and directrix.
In this lesson, Sasha and Keoni build upon the method that they developed in Lessons 3 and 4 of using the geometric definition of a parabola and the Pythagorean theorem to derive the equations for particular parabolas with vertex at (0,0). They generalized this method in Lesson 5 for a family of parabolas with vertex at the origin but an unknown distance between the vertex and focus (the p-value). In Lesson 8, they generalized the method to parabolas with a specific non-origin vertex. Finally, in this lesson, they derive the vertex form for a parabola by using parameters (h,k) for the vertex and an unknown p-value.
• CCSS.M.HSA.CED.A.2: Create equations in two or more variables to represent relationships between quantities; graph equations on coordinate axes with labels and scales.
The students build equations in two variables for different parabolas that capture a relationship between quantities. They represent these relationships on a coordinate grid system.
• CCSS.M.HSA.SSE.A.1.B: Interpret complicated expressions by viewing one or more of their parts as a single entity.
On a parabola with general vertex (h, k) and unknown p-value, Sasha and Keoni express the distance from a general point (x, y) to its directrix as y – k + p. They conceive of this distance as a single entity, which they locate on the graph. They are also able to describe and locate the distances represented by parts of the expression: y, k, p, and y – k.
Common Core Math Practices
CCSS.Math.Practice.MP2: Reason abstractly and quantitatively.
According to the Common Core’s description of Math Practice 2, mathematically proficient students are able to “decontextualize—to abstract a given situation and …manipulate the representing symbols as if they have a life of their own” and to “contextualize, to pause as needed during the manipulation process in order to probe into the referents for the symbols involved.” In Episode 7, Sasha and Keoni use the Pythagorean theorem to set up the equation for a given parabola as ((y–k)–p)2 + (x–h)2 = ((y–k)–p)2 and then reason abstractly by performing appropriate algebraic transformations to arrive at the equation y = (x–h)2/(4p) + K. However, they also reason quantitatively in Episode 6 by describing each term that they substituted into the Pythagorean theorem (namely, x – h, y – k + p, and y – k – p) as distances on the graph.



















