Home

Episode 6 Supports

  • Episode Description

    Exploring: Sasha and Keoni use the Pythagorean theorem to derive the equation for a parabola with the vertex at (0,0) and a focus p units above the vertex.

  • Focus Questions

    For use in a classroom, pause the video and ask these questions:

     

    1. [Pause video at 2:25]. What are the lengths of the vertical lines that Sasha and Keoni just drew?

     

    2. [Pause video at 6:09]. Finish writing the equation and then solve for y. [Then start the video again and stop at 7:58]. How did your solution method compare with Sasha and Keoni’s?

  • Supporting Dialogue

    Provide opportunities for all your students to express their ideas verbally, by asking them to talk with a partner.

     

    • [Pause the video at 3:58]. Talk with your neighbor. Where does the term y – p come from and what does it mean?

    • [Pause the video at 7:58]. Talk with your neighbor. Where does the equation y = x2/(4p)  come from? Where does the 4p come from?

  • Math Extensions

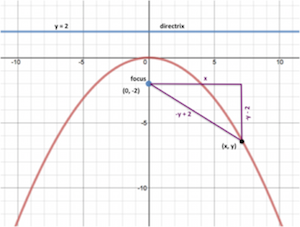
    1. Examine the parabola with a vertex at the origin and a focus at (0, -2). A general point on the parabola is labeled (x, y). A right triangle was formed so that the hypotenuse connects the (x, y) and the focus. The lengths of the three sides of the right triangle are x,
    -y + 2, and -y – 2. Explain why:

    1. the distance from (x, y) to the x-axis is -y.
    2. the length of the vertical side of the right triangle is -y – 2.
    3. the length of the hypotenuse of the right triangle is -y + 2.
    4. the length of the horizontal side of the right triangle is x.

     

    2a. Using the Pythagorean Theorem and the definition of a parabola, derive the equation of the parabola with a vertex at the origin and a focus at (0,-2).

     

    2b. Compare your equation with the equation that Keoni and Sasha derived for a parabola with a vertex at the origin and a focus at (0,2). What do you notice?


  •  

1

2

3

4

5

6

7

 

Mathematics in this Lesson

Lesson Description

Targeted Understanding

CC Math Standards

CC Math Practices

Lesson Description

 

Keoni and Sasha determine a general method for representing the equation for a parabola with a vertex on the origin and a focus p units above the vertex.

Targeted Understandings

 

This lesson can help students:

 

  • Interpret the meaning and use of an equation that they derive to represent a family of parabolas with vertex at the origin and focus p units above the vertex (y = x2/(4p)).

  • Conceive of the parameter p in the equation y =  x2/(4p)  as a distance between the vertex and focus of a parabola. The value of p can vary, but once it is set (e.g., when p = 2), then an equation is defined (e.g., y =  x2/8) that represents a unique parabola.

  • Relate geometric features of parabolas to elements of corresponding equations. For example, the equation y =  x2/8 can also be expressed as y =  x2/(2•4), where the 2 represents the number of units between the focus and vertex of the parabola.

Common Core Math Standards

• CCSS.M.HSG.GPE.A.2: Derive the equation of a parabola given a focus and directrix.

In Episode 6, Sasha and Keoni derive the equation (in two forms) for the family of parabolas with vertex (0,0) and focus p units above the vertex, namely y = x2/(4p)  and x = √(4py).  They do this by generalizing the method they used to develop an equation for a parabola with p = 1 in Lessons 3 and 4 (y =  x2/4 and x = √(4y)), for a parabola with p = 2 in Episode 2 of this lesson (y =  x2/8 and x = √(8y)), and for a parabola with p = 3 in Episode 4 (y =  x2/12 and x = √(12y)).

 

• CCSS.M.HSA.APR.A.1: Perform arithmetic operations on polynomials.

Sasha and Keoni multiply binomials, such as (y + 2)2 and (y + p)2, in service of deriving an equation for a particular parabola (in Episodes 2 and 4) or a family of parabolas (Episode 6).

 

 

 

Common Core Math Practices

 

CCSS.Math.Practice.MP7. Look for and make use of structure.

In this lesson, Sasha and Keoni make use of mathematical structure on two levels. First, they discern a pattern relating the equations of three parabolas (y = x2/4, y = x2/8, and y =  x2/12) with the corresponding distance between the vertex and focus (respectively, p = 1; p = 2; and p = 3).  Specifically, they see the structure of 1•4, 2•4 and 3•4 in the denominators of their equations, which is the p-value of the parabola multiplied by 4. Consequently Keoni and Sasha conjecture that the general equation of a parabola with vertex (0,0) and focus p units above the vertex will be y = x2/(4p).  Then they look for and make use of structure on a second level. To derive the equation y =  x2/(4p), they need to identify the lengths of the sides of a right triangle with hypotenuse connecting a general point on the parabola with the focus. To accomplish this challenging task, Sasha and Keoni see a pattern in similar quantities that they identified for particular parabolas, which they generalize to define lengths involving the parameter p, such as  y – p and y + p.