Home

Episode 1 Supports

  • Episode Description

    Making Sense: Sasha and Keoni examine the similarities and differences between two parabolas with vertices on the origin but with different distances to the focus. They determine if the same equation could represent both parabolas.

     

  • Students’ Conceptual Challenges

    Keoni wonders if a single equation (y = x2/4) could represent two different parabolas [1:34].

     

    • Sasha disagrees with Keoni. They resolve their dispute by testing the coordinates of points on each of the parabolas in the given equation. They conclude that the two parabolas will have unique equations.

  • Focus Questions

    For use in a classroom, pause the video and ask these questions:

     

    1. [Pause video at 3:38]. What else do you notice about the given points and their relationships to the focus and the directrix of each parabola?

     

    2. [Pause video at 5:04]. Which equation did Sasha just use? What does she mean by “it works”?

  • Supporting Dialogue

    Focus students’ attention on conjecturing and providing evidence for their conjectures:

     

    1. Name some other coordinates on the blue parabola. Explain how you know that they are on the blue parabola.

    2. How might you predict other values on the blue parabola? What evidence are you using to make your predictions?

  • Math Extensions

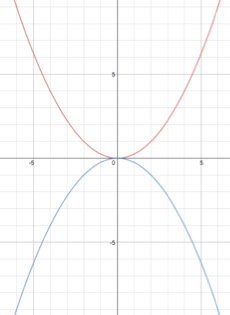
    1. Consider the two parabolas graphed below. How are they different? How are they the same?

     

    2. Can you determine the focus and directrix of each parabola? Explain your thinking.

     

    ​

  •  

1

2

3

4

5

6

7

 

Mathematics in this Lesson

Lesson Description

Targeted Understanding

CC Math Standards

CC Math Practices

Lesson Description

 

Keoni and Sasha determine a general method for representing the equation for a parabola with a vertex on the origin and a focus p units above the vertex.

Targeted Understandings

 

This lesson can help students:

 

  • Interpret the meaning and use of an equation that they derive to represent a family of parabolas with vertex at the origin and focus p units above the vertex (y = x2/(4p)).

  • Conceive of the parameter p in the equation y =  x2/(4p)  as a distance between the vertex and focus of a parabola. The value of p can vary, but once it is set (e.g., when p = 2), then an equation is defined (e.g., y =  x2/8) that represents a unique parabola.

  • Relate geometric features of parabolas to elements of corresponding equations. For example, the equation y =  x2/8 can also be expressed as y =  x2/(2•4), where the 2 represents the number of units between the focus and vertex of the parabola.

Common Core Math Standards

• CCSS.M.HSG.GPE.A.2: Derive the equation of a parabola given a focus and directrix.

In Episode 6, Sasha and Keoni derive the equation (in two forms) for the family of parabolas with vertex (0,0) and focus p units above the vertex, namely y = x2/(4p)  and x = √(4py).  They do this by generalizing the method they used to develop an equation for a parabola with p = 1 in Lessons 3 and 4 (y =  x2/4 and x = √(4y)), for a parabola with p = 2 in Episode 2 of this lesson (y =  x2/8 and x = √(8y)), and for a parabola with p = 3 in Episode 4 (y =  x2/12 and x = √(12y)).

 

• CCSS.M.HSA.APR.A.1: Perform arithmetic operations on polynomials.

Sasha and Keoni multiply binomials, such as (y + 2)2 and (y + p)2, in service of deriving an equation for a particular parabola (in Episodes 2 and 4) or a family of parabolas (Episode 6).

 

 

 

Common Core Math Practices

 

CCSS.Math.Practice.MP7. Look for and make use of structure.

In this lesson, Sasha and Keoni make use of mathematical structure on two levels. First, they discern a pattern relating the equations of three parabolas (y = x2/4, y = x2/8, and y =  x2/12) with the corresponding distance between the vertex and focus (respectively, p = 1; p = 2; and p = 3).  Specifically, they see the structure of 1•4, 2•4 and 3•4 in the denominators of their equations, which is the p-value of the parabola multiplied by 4. Consequently Keoni and Sasha conjecture that the general equation of a parabola with vertex (0,0) and focus p units above the vertex will be y = x2/(4p).  Then they look for and make use of structure on a second level. To derive the equation y =  x2/(4p), they need to identify the lengths of the sides of a right triangle with hypotenuse connecting a general point on the parabola with the focus. To accomplish this challenging task, Sasha and Keoni see a pattern in similar quantities that they identified for particular parabolas, which they generalize to define lengths involving the parameter p, such as  y – p and y + p.